This presentation is designed to detail an additional tool which can be used to make trading systems more self adaptive and therefore more responsive to current market conditions.
If a system uses back data to any degree it can be regarded as being self adaptive to one degree or another. Moving averages, standard deviations, breakouts, neural networks, etc. all rely on some historical price movement to generate buy and sell signals.
This programming technique takes the self adaptive concept one step farther by using the system itself to adjust its own trading parameters for each trade.
I wish to emphasize at the beginning that this is a programming technique which must be applied in a different manner to each and every system on which it is used. It is not a canned function or add on program which can be applied to any system.
Also, since the programming involved in the application of this technique can be quite involved and extensive, it should be emphasized that this is not a fix - all for mediocre or poor systems. In fact, it will probably worsen the results of a poor system since the variables will constantly be reset to extreme values, making the equity swings of the system even more pronounced.
Systems which respond best to this technique are those which are considered robust in nature and remain profitable over a progressive set of input variables. Such a system should show a bell curve pattern when the results of an optimization over the critical inputs is performed. Systems which respond well to frequent optimization will find this technique useful in improving performance and smoothing out equity curves.

BackTest Regular Optimization

Traders and system developers regularly check variations of their system against recent back data in an attempt to discover if an underlying change in the market has effected the performance of their system. Done properly, this effort can be rewarded with improved system performance real - time. Improperly done, which is more often the case, frequent re - optimization leads to a system which is overly curve fitted and more prone to losses.
The difficulty is knowing how often to optimize, over what system parameters and how much data should be used for each test. To come up with the correct testing parameters is a time consuming operation since there are so many variables to consider. Also, if the testing is to be accurate, a fairly large volume of past data should be considered.
Through the use of parallel functions, one can set up a group of indicators which will graphically depict to the user when a significant change has occurred in the manner in which the system is responding to changes in market personality. Additionally, if warranted by indicator observation, the system can be altered to automatically change variable values when indicated by changes in the market.
In this manner one is able to observe what the results of the system would have been had re-optimization occurred at regular, defined intervals over specified input values.

Developmental History

When I began designing systems for currency trading in TradeStation several years ago I was quick to notice that the optimal variables which controlled the system equations would vary greatly from one contract month to another. My initial methodology involved an early range breakout system for trading the currency markets whereby the system would place breakout buy or sell stops slightly outside the early market range. Since the definition of the early range was critical to system performance, variables were used in the system to set the range by time of day, width of the early range, and the proximity of the current price to extreme range when the early range was defined.
It was soon obvious that the best settings for the variables used to define the critical early range varied significantly from contract to contract. Even averaging the variables over several contracts produced only mediocre results. Obviously there was a characteristic somewhere in the activity of the market that was fluctuating regularly which resulted in the radical activity of the system. Also obviously, if the system was to be profitable in the future, I was going to get a handle on the root of these fluctuations. One could always optimize the variables for each contract and make the system look like the best thing around but we all know by now that curve fitting is a quick way to overconfidence and a losing system.
For months I analyzed every market parameter I could define - gaps, average daily range, daily open to close, ratios of high to low to open to close, tendency of a quiet day to follow a wild day, changes of market activity around big report days, and so on. Although measuring these parameters and using them to adjust the system variables was of some benefit to system performance, I was still unable to achieve the consistency across all data that I desired.
Then one day it dawned on me - the best way to evaluate the market with respect to a particular system is the system itself! By running the system against a defined subset of past market data using a defined set of variables one could constantly monitor the performance of the system across all variable settings. Properly programmed, the system could constantly adjust critical variables to reflect optimum performance against recent market data.
This technique operates in much the same fashion in which the pure market technician assesses the market. The pure technician ignores all fundamentals, confident that eventually all forces impacting on the market will be reflected in price. In much the same way, a parallel user function ignores all the myriad of technical forces in the market as they impact the system and concentrates only on the net effect of these changes in market characteristic on the system itself. Rather than trying to determine which phase of market activity is impacting the results of the system, we use the system itself to monitor changes in the market personality and make system adjustments accordingly.
To accomplish this formidable task I created what I have chosen to call a parallel user function.

Programming Examples

A parallel function is one which is written to mimic the base system in every respect. At first this might seem simple, as one could simply copy the entire system code and save it as a function. However, system functions such as buy, sell, exitlong, exitshort, marketposition, positionprofit, are not available for use in functions. You must therefore write your function to perform as a system without the use of these extremely useful commands.

To clarify and illustrate the usefulness of this technique let's develop a simple breakout system and the apply the parallel function to the system.

Our system will involve the simple breakout of a range at a given time early in the trading day. We'll keep track of the high and low of the day and at a given, input selectable time, we'll place a breakout buy above the range of the day and a breakout sell below the established range. We'll then take profit at a user selectable target and set our stop loss, again with a user selectable value.

Base System

Here's the EasyLanguage code for our system. I'll explain what each section and then compare the system code with that required for the parallel function.

Download the .ela code for this system.

Inputs: Delay(45), Tgt(7), Stp(4);

Vars: NuHi(0), NuLo(0), Bpt(0), Spt(0);

If D<>D[1] then begin

NuHi = H;
NuLo = L;
Bpt = 9999999;
Spt = 0;

end;

If H>NuHi then NuHi = H;
If L<NuLo then NuLo = L;

If T = CalcTime(Sess1StartTime,Delay) then begin

Bpt = NuHi +.1;
Spt = NuLo - .1;

end;

If TradesToday(d) = 0 then begin;

BUY Bpt stop;

SELL Spt stop;

end;

If MarketPosition = 1 then begin
Exitlong("L_ TGT") entryprice + tgt limit;
ExitLong("L_Stp") entryprice - Stp stop;
end;

If MarketPosition = -1 then begin
ExitShort("S_Tgt") entryprice - tgt limit;
ExitShort("S_Stp") entryprice + stp stop;
end;

**********

System Code Explanation

The first lines are the input and variable declarations.
"Delay" refers to the number of minutes after the open of the market that the range determination will be made. In this example, the input is defaulted to 30, meaning the system will buy or sell the range established 30 minutes after the open of the market. "Tgt" is the objective of the trade, or "target" price, expressed in points. In this example the target is two points in the S&P, or $500.00. "Stp" is the value of the stop loss for the system, in this example, four S&P points.
The variables NuHi and NuLo will track the expanding high and low for the day. The Bpt and Spt variables will store the calculated buy and sell points for the system.

Inputs: Delay(30), Tgt(2), Stp(4);

Vars: NuHi(0), NuLo(0), Bpt(0), Spt(0);

Resets. The NuHi and NuLo variables, which progressively record the high and low for the day as the range expands, are reset to the high and low of the first bar of the day. The buy point (Bpt) and sell point (Spt) are reset outside the range of the market to prevent premature buy and sell signals.

If D<>D[1] then begin

NuHi = H;
NuLo = L;
Bpt = 9999999;
Spt = 0;

end;

These two lines record the high and low for the day as the range expands and stores them in the NuHi and NuLo variables.

If H>NuHi then NuHi = H;
If L<NuLo then NuLo = L;

This bracket uses the CalcTime function set the breakout time for the system using the Delay input. The buy point and sell point are set to the high and low for the day at that time, plus or minus 1 tick, respectively.

If T = CalcTime(Sess1StartTime,Delay) then begin

Bpt = NuHi;
Spt = NuLo;

end;

This is the area of the code which executes the buy and sell orders for the system, taking only one trade per day. The systems issues orders to buy one tick above the high or sell one tick below the low of the day.

If TradesToday(d) = 0 then begin;

BUY Bpt stop;

SELL Spt stop;

end;

These next two brackets are the exit routines for the system. In the first bracket, the system exits a long position at the entry price plus the target input in the case of a profitable trade or will exit at the entryprice - the stop input in the case of a stopped out position.

The second bracket exits the short positions in a similar manner, with profit being taken at the entry price minus the target price and the system suffering a stopped out loss at the entryprice plus the stop price.

If MarketPosition = 1 then begin
Exitlong("L_ TGT") entryprice + tgt limit;
ExitLong("L_Stp") entryprice - Stp stop;
end;

If MarketPosition = -1 then begin
ExitShort("S_Tgt") entryprice - tgt limit;
ExitShort("S_Stp") entryprice + stp stop;
end;

Programming the Parallel Function

Download the .ela code for this function.

Now, let's detail the programming of the parallel function which must behave exactly as the system but without the use of the system statements buy, sell, exitlong and exitshort.

Here's the parallel function, which I've named OMW_BO (for Omega World Breakout).

Inputs: Delay(numeric), Tgt(numeric), Stp(numeric);

Vars: NuHi(0), NuLo(0), Bpt(0), Spt(0), tt(0), Lng(false), Sht(false);

If D<>D[1] then begin

NuHi = H;
NuLo = L;
Bpt = 9999999;
Spt = 0;
Lng = false;
Sht = false;
Value1 = 0;
tt = 0;

end;

If H>NuHi then NuHi = H;
If L<NuLo then NuLo = L;

If T = CalcTime(Sess1StartTime,Delay) then begin

Bpt = NuHi + .1;
Spt = NuLo - .1;

end;

If H > Bpt and tt = 0 then Lng = true;

If Lng then begin

If L < Bpt - Stp and lng[1] = true then begin
If tt = 0 then Value1 = tgt;
tt = 1;
end;
If L < Bpt - Stp then begin
If tt = 0 then Value1 = -stp;
tt = 1;
end;

If tt = 0 and T = Sess1EndTime then Value1 = C - Bpt;

end;

If L < Spt and tt = 0 then sht = true;

If sht then begin

If L < Spt - tgt then begin
If tt = 0 then Value1 = tgt;
tt = 1;
end;
If H >= Spt + stp and sht[1] = true then begin
If tt = 0 then Value1 = -stp;
tt = 1;
end;

If tt = 0 and T = Sess1EndTime then Value1 = Spt - C;

end;

OMW_BO = Value1;

Now, lets detail the parallel function code, pointing out the changes necessary to enable the function to perform as a system.

The input declarations are similar, except that the default values are set up to receive numeric inputs from the indicator / system using this function.

Inputs: Delay(numeric), Tgt(numeric), Stp(numeric);

In the variables declaration section the first 4 variables are identical. It is necessary to add three more variables for our function: tt, which will record total trades, Lng and Sht, which will be reset to true if the market takes a long "Lng" or short "Sht" position.

Vars: NuHi(0), NuLo(0), Bpt(0), Spt(0), tt(0), Lng(false), Sht(false);

The reset section adds reset lines for the newly added variables as they will need to store new values for each new day. We also reset value1 to 0 here which stores the ultimate value for the function.

If D<>D[1] then begin

NuHi = H;
NuLo = L;
Bpt = 9999999;
Spt = 0;
Lng = false;
Sht = false;
Value1 = 0;
tt = 0;

end;

The next six lines are identical to the system code.

If H>NuHi then NuHi = H;
If L<NuLo then NuLo = L;

If T = CalcTime(Sess1StartTime,Delay) then begin

Bpt = NuHi + .1;
Spt = NuLo - .1;

end;

Here's where the major changes begin.
The next line tells the function when a long breakout has occurred. The statement says that if the high of a bar is greater than our buy point then the market has traded through our buy stop and system is in a long position. Additionally, since our system is designed to take only one trade per day, the tt=0 statement will only allow the Lng variable to be set to true if this is the first time that the high of a bar goes through our buy point.

If H > Bpt and tt = 0 then Lng = true;

Inside the next bracket we calculate the results of our long trade.

If Lng then begin

The next line is activated when the high of a bar exceeds our buy point plus our target objective, or when our system has taken a profit on the long position. If this condition (H > Bpt + Tgt) is true then the program returns the value of the target for value1 (Value1 = tgt), only if we are on the first occurrence of the breakout (tt=0). Therefore, the function will return the value for the target stop when the high of a bar has exceeded the breakout point plus the target value.
The last line in this bracket (tt = 1) sets the total trades to 1 which prevents the function from reporting any more values for the day.

If H > Bpt + Tgt then begin
If tt = 0 then Value1 = tgt;
tt = 1;
end;

The next bracket calculates a function value when the system is stopped out for a loss. In the same fashion as the bracket above, the function value is set to the value of the stop loss (stp) when the low of a bar goes below our buy point minus the stop loss value.

If L < Bpt - Stp and lng[1] = true then begin
If tt = 0 then Value1 = -stp;
tt = 1;
end;

The last line in this bracket returns the result of the system should we reach the end of the day and the position is liquidated on the close.

If tt = 0 and T = Sess1EndTime then Value1 = C - Bpt;

end;

The next several lines of the function program calculate the value for the function in the case of a short position for the system.

If L < Spt and tt = 0 then sht = true;

If sht then begin

If L < Spt - tgt then begin
If tt = 0 then Value1 = tgt;
tt = 1;
end;
If H >= Spt + stp and sht[1] = true then begin
If tt = 0 then Value1 = -stp;
tt = 1;
end;

If tt = 0 and T = Sess1EndTime then Value1 = Spt - C;

end;

The last line assigns to the function the calculated value for value1.

OMW_BO = Value1;

De Bugging Tips

It's always a good idea to plot the function as an indicator as you are going through the programming process. Your goal is to program the function to perform exactly as the base system. Plotting it as an indicator on the same chart as the system makes the comparison between the function and the system more manageable.
First, set the system to 0 zero commission and slippage so the system reports are the actual result of the trade. Also, multiply the point return for the function by the big point value so the value of the function will match the return from the system. You can then use the system report window and the data window to compare the results of the function and the system. You must be certain to have the inputs identical for the system and the function. Also, you must use the same Max Bars Back settings - don't make the mistake of using the auto detect feature for this parameter on your indicator.
The plot for the indicator should change each time the system completes a trade. The change in the indicator plot should be idential to the change inthe system result.
It is important that you check the performance of your function against every possible trade. For just our simple system, you'll need to check the accuracy of 5 separate types of trades - the long profit, long stop out, short profit, short stop out and the end of day exit. It is necessary to check each trade against the function since their are separate lines of code for each potential system outcome, all of which could contain errors.
One could logically ask at this point - why not just use the System Equity Indicator to check the progress of the system? The differences between the two approaches is that the system equity indicator only measures the performance of the system currently being run on the chart. Our approach utilizing the power of the parallel function gives us the flexibility to check various system settings against each other oer the life of the chart to get a reading of system behavior under varying market conditions.

Initial Use of the Parallel Function

Now that we've programmed our function let's put it to work evaluating our system on a day by day basis.
The first use of the function should be as an indicator which plots multiple versions of the system. Here's the code for an indicator which plots the progressive results of our system using 8 different profit target levels. Obviously, you would need to write two separate indicators with 4 plots each to display all 8 system configurations as only 4 plots per indicator are allowed.
Normally when one plots a function in an indicator you would supply all the function inputs using indicator inputs. However, in this particular instance, we will be entering different values in the indicator programming so that several variations of our system outputs will be displayed. Later I will illustrate a more complex indicator in which all variations of the system can be plotted using multiple inputs.
In this indicator we're using two arrays ("Bsys" and "BsysT" ) to store the results of the various system variations as the function generates results for each day on the chart.
Note, in the 8 lines immediately following the array declarations, that we use a separate function call for each system variation and store it in a separate array position. For each function call, the delay and stop inputs remain static, using the input supplied values. In this example I have entered values 5 through 12 for the target input. This has the result of calculating the results of our system for 8 different profit targets each day.
The next 8 lines simply increment the proper array positions in the BsysT array each time the function calculates a new value for each system variation.

Download the .ela code for this indicator.

Input: DELAY(45),STP(4);

Arrays: BSys[8](0), BSysT[8](0);

BSys[1] = OMW_BO(DELAY,5,STP);
BSys[2] = OMW_BO(DELAY,6,STP);
BSys[3] = OMW_BO(DELAY,7,STP);
BSys[4] = OMW_BO(DELAY,8,STP);
BSys[5] = OMW_BO(DELAY,9,STP);
BSys[6] = OMW_BO(DELAY,10,STP);
BSys[7] = OMW_BO(DELAY,11,STP);
BSys[8] = OMW_BO(DELAY,12,STP);

If BSys[1] <> Bsys[1][1] then BSysT[1] = BSysT[1] + BSys[1];
If BSys[2] <> Bsys[2][1] then BSysT[2] = BSysT[2] + BSys[2];
If BSys[3] <> Bsys[3][1] then BSysT[3] = BSysT[3] + BSys[3];
If BSys[4] <> Bsys[4][1] then BSysT[4] = BSysT[4] + BSys[4];
If BSys[5] <> Bsys[5][1] then BSysT[5] = BSysT[5] + BSys[5];
If BSys[6] <> Bsys[6][1] then BSysT[6] = BSysT[6] + BSys[6];
If BSys[7] <> Bsys[7][1] then BSysT[7] = BSysT[7] + BSys[7];
If BSys[8] <> Bsys[8][1] then BSysT[8] = BSysT[8] + BSys[8];

Plot1(BSysT[1],"BSys1");
Plot2(BSysT[2],"BSys2");
Plot3(BSysT[3],"BSys3");
Plot4(BSysT[4],"BSys4");

Plot1(BSysT[5],"BSys5");
Plot2(BSysT[6],"BSys6");
Plot3(BSysT[7],"BSys7");
Plot4(BSysT[8],"BSys8");

Now we're ready to plot our indicator and view the results. It will be necessary to plot two indicators, as mentioned above. Plot both in the same subgraph, choosing a different color for each plot. It is also necessary to set the scaling of both indicators to the same user - defined parameters to assure all plots can be compared to each other on an equal basis.

In the chart above you will see the results of our indicator. On this example the system settings are for a 7 point profit target while using a 4 point stop.
The results for each of our 8 system settings are displayed as a separate tracing in subgraph two of the chart, each with a different color. Remember that we are only varying the system in the indicator by a single parameter, the profit target for the system.
Bsys1 = 5 point objective; Bsys2 = 6 point objective; Bsys3 = 7 point objective; Bsys4 = 8 point objective; (black) Bsys5 = 9 point objective; Bsys6 = 10 point objective; Bsys7 = 11 point objective; Bsys8 = 12 point objective;
With that in mind, note how the indicator positions change along with the system exits. Also, note that there is considerable difference in performance across all settings of the system as displayed by our indicator. It is of particular interest to note the indicator patterns on days when some system settings would have been profitable and some would have had losses.
For instance, look at the results on 2/16. The system sold the market at 1243.90 on a stop and took profit 7 points lower at 1236.90. Note that the indicator tracings representing profit objectives of 7 points or less also took a profit while those with greater objectives recorded losses when that system setting was stopped out at the 4 point stop loss point.
A similar pattern emerges on 2/19 when two of the simulated systems took losses when the market failed to reach their greater objectives, pulled back and eventually stopped these options out near the end of the day.
Although it is not evident on this small snapshot of the system screen, the most absorbing observation is to watch the different systems gain and lose to each other as the days progress. While it is not always evident what changes are taking place in the market to cause these variations, it becomes readily evident when there is a change in market personality developing. Again, recall that we are only measuring a single variable of system performance, that of our profit target. When other parameters such as time of breakout and the stop loss level are also included the variations of system performance become more dramatic and subsequently more revealing of the response of the system to the underlying market activity.
The next step is to construct similar indicators for the other two parameters, namely the delay input and the stop input. It is then possible to assess each input over 8 different settings dynamically as the chart moves along.
Finally, we'll construct an indicator with user selectable inputs for each parameter so the user can construct up to 4 system following plots based on the results of the observations of the first 3 indicators.

Below is the code for out indicator which will plot 8 different system simulations for the delay input in the system. Note that we provide user selectable inputs for the starting value of the delay period as well as an incremental factor (Delay_Inc) for the input, in much the same fashion that is used when one does an optimization.

Note that the code below calls our parallel function for each of the 8 simulations of the system, providing an input for the delay factor which starts with the beginning value (Delay_Start) and increments each

Download the .ela code for this indicator.

Input: Delay_Start(30),Delay_Inc(5),Tgt(5),Stp(4);

Vars: Pts(0), TTlPts(0);

Arrays: BSys[8](0), BSysT[8](0);

BSys[1] = OMW_BO(Delay_Start + (Delay_Inc*0),Tgt,Stp);
BSys[2] = OMW_BO(Delay_Start + (Delay_Inc*1),Tgt,Stp);
BSys[3] = OMW_BO(Delay_Start + (Delay_Inc*2),Tgt,Stp);
BSys[4] = OMW_BO(Delay_Start + (Delay_Inc*3),Tgt,Stp);
BSys[5] = OMW_BO(Delay_Start + (Delay_Inc*4),Tgt,Stp);
BSys[6] = OMW_BO(Delay_Start + (Delay_Inc*5),Tgt,Stp);
BSys[7] = OMW_BO(Delay_Start + (Delay_Inc*6),Tgt,Stp);
BSys[8] = OMW_BO(Delay_Start + (Delay_Inc*7),Tgt,Stp);

   If BSys[1] <> Bsys[1][1] then BSysT[1] = BSysT[1] + BSys[1];
   If BSys[2] <> Bsys[2][1] then BSysT[2] = BSysT[2] + BSys[2];
   If BSys[3] <> Bsys[3][1] then BSysT[3] = BSysT[3] + BSys[3];
If BSys[4] <> Bsys[4][1] then BSysT[4] = BSysT[4] + BSys[4];
   If BSys[5] <> Bsys[5][1] then BSysT[5] = BSysT[5] + BSys[5];
   If BSys[6] <> Bsys[6][1] then BSysT[6] = BSysT[6] + BSys[6];
   If BSys[7] <> Bsys[7][1] then BSysT[7] = BSysT[7] + BSys[7];
   If BSys[8] <> Bsys[8][1] then BSysT[8] = BSysT[8] + BSys[8];

   Plot1(BSysT[1],"Delay1");
   Plot3(BSysT[3],"Delay2");
   Plot2(BSysT[2],"Delay3");
   Plot4(BSysT[4],"Delay4");

   Plot1(BSysT[5],"Delay5");
   Plot2(BSysT[6],"Delay6");
   Plot3(BSysT[7],"Delay7");
      Plot4(BSysT[8],"Delay8");

The indicator on the above chart depicts graphically the results of 8 simulations of our system as plotted by the parallel function. The tracings depict the results of the system over 8 different breakout times as entered into the indicator by the function calls. The initial input of a 30 minute delay is incremented by the input factor of 5 for each successive simulated plot. Thus, plot Delay1 reflects the system with a breakout time 30 minutes after the open. Delay2 plots the system with a 35 minute delay, Delay3 equals a 40 minute delay, etc. Again, note the variations evident between the different system simulations. Although the purple tracing, representing a system simulation with a breakout of the range established 55 minutes after the open, is the superior setting at this particular time, examination of the remainder of the chart will demonstrate that other settings are superior at other times. Note how several of the simulations continually compete with each other for the best performance. By plotting several indicators on chart, each representing simulations of several settings of different system parameters, the system developer or trader can get a graphic representation of the behavior of the system under constantly changing market conditions.

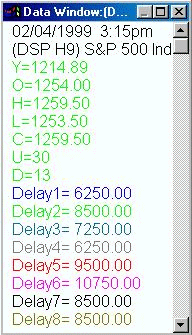
The data window at right depicts the results of all 8 systems simulated in the chart above. Being aware of the settings in the indicator inputs, we know that Delay 1 represents a breakout of a range established 30 minutes after the market open. Each successive simulation represents a breakout range set up 5 minutes later than the preceding graphic. All other system parameters, the target and stop, remain static so
the system can be measured accurately with the breakout range time being the only variable which is responsible for the changes in the system reports in the window at right.The numbers reported in the data window are the actual dollar amounts which would have been generated by the system under each progressively incremented breakout time setting.

The indicator code below is identical to the previous program with the only exception being that the stop parameter of the system is being increased incrementally for each system simulation. The stop settings begin at 4 points, as determined by the input, and are increased by the Stop_Inc amount for each successive function call.

Input: Delay(45),Tgt(5),Stp_Start(4), Stop_Inc(1);

Vars: Pts(0), TTlPts(0);

Arrays: BSys[8](0), BSysT[8](0);

BSys[1] = OMW_BO(Delay,Tgt,Stp_Start + (Stop_Inc*0));
BSys[2] = OMW_BO(Delay,Tgt,Stp_Start + (Stop_Inc*1));
BSys[3] = OMW_BO(Delay,Tgt,Stp_Start + (Stop_Inc*2));
BSys[4] = OMW_BO(Delay,Tgt,Stp_Start + (Stop_Inc*3));
BSys[5] = OMW_BO(Delay,Tgt,Stp_Start + (Stop_Inc*4));
BSys[6] = OMW_BO(Delay,Tgt,Stp_Start + (Stop_Inc*5));
BSys[7] = OMW_BO(Delay,Tgt,Stp_Start + (Stop_Inc*6));
BSys[8] = OMW_BO(Delay,Tgt,Stp_Start + (Stop_Inc*7));

If BSys[1] <> Bsys[1][1] then BSysT[1] = BSyst[1] + BSys[1];
If BSys[2] <> Bsys[2][1] then BSysT[2] = BSyst[2] + BSys[2];
If BSys[3] <> Bsys[3][1] then BSysT[3] = BSyst[3] + BSys[3];
If BSys[4] <> Bsys[4][1] then BSysT[4] = BSyst[4] + BSys[4];
If BSys[5] <> Bsys[5][1] then BSysT[5] = BSyst[5] + BSys[5];
If BSys[6] <> Bsys[6][1] then BSysT[6] = BSyst[6] + BSys[6];
If BSys[7] <> Bsys[7][1] then BSysT[7] = BSyst[7] + BSys[7];
If BSys[8] <> Bsys[8][1] then BSysT[8] = BSyst[8] + BSys[8];

Plot1(BSysT[1]*250,"Stop1");
Plot2(BSysT[2]*250,"Stop2");
Plot3(BSysT[3]*250,"Stop3");
Plot4(BSysT[4]*250,"Stop4");

The indicator on chart above represents the results of the system using 8 progressively incremented settings for the stop input. As before, the inputs for the other two parameters are held static so the graphs are representative of the system changes as effected only by the changing stop input.

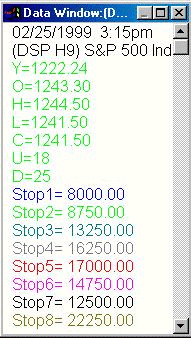
As with the delay input indicator, the data window on the right reports the system results under 8 different settings for the stop parameter of our system.At this point on the chart the stop setting with the highest value, or 11 points, is giving the best system results with the delay input frozen at 45 minutes after the open and the target for the system set at 5 points.

Putting It All Together

Now that we’ve completed the parallel function and given a few examples of its operation on selected system inputs, lets put the indicator portion of the puzzle together in a form which will allow more thorough system testing.
The code below allows 3 inputs for all three critical variables of the system – delay, target and stop. The inputs allow the user to select a starting value for each variable from which the system analysis will begin. An incremental value can also be entered for each variable allowing the indicator to calculate 8 simulations for each variable.
By observing the individual plots for delay, target and stop the user now has a fairly good idea of which settings are going to be best for the optimal performance of the system, but up to now has not been able to observe the multiple system analysis across all inputs. With this next step, the user can enter a range of settings for each variable according to the observations from the previous indicator plots and then observe indicator readings representative of the total system using a varied range of variable inputs.

Input: Delay_Start(45),Delay_Inc(5),Tgt_Start(5),Tgt_Inc(1),Stp_Start(4), Stop_Inc(1);

Vars: Pts(0), TTlPts(0);

Arrays: BSys[8](0), BSysT[8](0);

BSys[1] = OMW_BO(Delay_Start + (Delay_Inc*0),Tgt_Start + (Tgt_Inc*0),Stp_Start + (Stop_Inc*0));
BSys[2] = OMW_BO(Delay_Start + (Delay_Inc*1),Tgt_Start + (Tgt_Inc*1),Stp_Start + (Stop_Inc*1));
BSys[3] = OMW_BO(Delay_Start + (Delay_Inc*2),Tgt_Start + (Tgt_Inc*2),Stp_Start + (Stop_Inc*2));
BSys[4] = OMW_BO(Delay_Start + (Delay_Inc*3),Tgt_Start + (Tgt_Inc*3),Stp_Start + (Stop_Inc*3));
BSys[5] = OMW_BO(Delay_Start + (Delay_Inc*4),Tgt_Start + (Tgt_Inc*4),Stp_Start + (Stop_Inc*4));
BSys[6] = OMW_BO(Delay_Start + (Delay_Inc*5),Tgt_Start + (Tgt_Inc*5),Stp_Start + (Stop_Inc*5));
BSys[7] = OMW_BO(Delay_Start + (Delay_Inc*6),Tgt_Start + (Tgt_Inc*6),Stp_Start + (Stop_Inc*6));
BSys[8] = OMW_BO(Delay_Start + (Delay_Inc*7),Tgt_Start + (Tgt_Inc*7),Stp_Start + (Stop_Inc*7));

Plot1(BSysT[1]*250,"Best1");
Plot2(BSysT[2]*250,"Best2");
Plot3(BSysT[3]*250,"Best3");
Plot4(BSysT[4]*250,"Best4");
{end;}

The chart above identifies the results of simulated testing across all three system variables, each with its own starting value and incremental values.

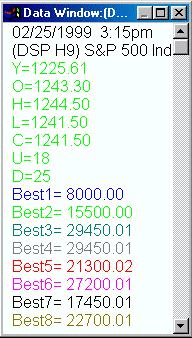
The box at right lists the results of each of our 8 system simulations as of the date at the top of the window. Each is color coded to one of the plots in the above chart.By being aware of the inputs for the indicator, one can graphically determine which settings were optimal for the system at any one given time through the course of the chart.For instance, on the date shown, 2-25-99, the magenta simulation, reflecting system settings of 75, 11 and 10 for delay, target and stop respectively, is showing the best overall net profit for the system with a net of $29,450 for the period beginning 1-5-99.It is also obvious from the results presented that the system we have developed here meets our criteria of a robust system as the results of a wide array of variable settings produce a smooth progression of values. Note that there are no settings which greatly outdistance any of the others, assuring us that the system results are not the result of one system setting catching a huge trade which accounts for the majority of the profits for the system.

The Final Step

Now that we’ve demonstrated the capabilities of a parallel function, the next step is to develop an automated system to take advantage of these functions.
Our goal is to create a system which will use parallel functions to constantly adjust its trading patterns in response to the ever changing personality of the market. In a sense, these systems could be thought of as self optimizing.
The programming here is based around the use of loops and arrays to test all the available options of inputs as selected by the user. It is also possible to restrict the self testing by the system to a set parameter, such as the number of days, number of trades, etc. For instance one could self – optimize the system for the last 30 days, the last 10 trades, the last 5 winning trades, etc. The possibilities for self testing are limited only by ones imagination once the parallel function is created.
In all cases, it is possible to program the system to test itself against a pre defined set of back data and, after determining the optimal set of variables for the current period, install these variable sets into the system equations so that they will be used for the next trade.
The advent of TradeStation 2000i has broadened the scope of this technique exponentially with the ability to manipulate arrays from within a user function and the elimination of the 64 K file size for system code. As time goes on we will no doubt find expanded uses for parallel functions with the vastly increased capability offered by 2000i.

Summary

Parallel functions can be a useful tool for both system development and testing.
The ultimate use for this tool is found in the creation of systems which are ultimately self adaptive in that they can use their own reaction to current market conditions to change their trading parameters on the fly.
It cannot be emphasized enough that this technique is by no means a fix – all for a mediocre or poor system. In fact, it will probably decrease the performance of such a system.
In the final analysis, the user will find this technique useful as an additional tool to make his or her trading more reactive to current market conditions.

By John F. Clayburg

JOHN WILEY & SONS, INC.
New York Chichester Weinheim Brisbane Singapore Toronto
ISBN: 0-471-41482-4
June 2001
320 Pages
Hard Cover
Description
Annotations
Contents
Reader's Comments
Support Pages
Order Form